RAPPORTO MATEMATICA-MUSICA DAL TEMPO DI
PITAGORA
Il primo tentativo di scala musicale lo si deve al filosofo-matematico Pitagora.
Utilizzando un monocordo e le proprietà delle frazioni (essendo, inoltre, che la sua dottrina prevedeva il numero come "essenza di tutte le cose") costruì la prima scala musicale "teorizzata". essa è però puramente "formale" perché sebbene sia "quadrata" dal punto di vista numerico dei rapporti tra le varie note che la compongono, all'orecchio risulta essere alquanto sgradevole. In effetti, il problema dell' accordatura è così "di base" che sovente non viene neanche rilevato. Eppure le singole note, che troviamo sulla tastiera di un pianoforte così come su quella di un flauto, costituiscono l'alfabeto con cui costruire una qualunque composizione musicale.
La domanda che sorge spontanea è con quale criterio sono stati scelti proprio quei suoni e, soprattutto, come sono state determinate le distanze tra uno e l' altro? In genere, quando si suddivide un intervallo continuo lo si fa con punti equidistanti, e infatti, come attestano vari strumenti musicali antichi, alcuni tentativi si mossero in questa direzione.
Essa tuttavia fu presto abbandonata, perché il criterio che è alla base della scelta dei suoni non è quello spaziale di equidistanza, bensì quello musicale di consonanza. Questo concetto, nei manuali di teoria, è così definito: un intervallo tra due note si dice consonante se, suonando le due note simultaneamente, si ottiene un effetto di gradevolezza e di quiete; si dice invece dissonante se produce un senso di instabilità e di tensione.
I termini impiegati ("gradevolezza", "tensione", "quiete") possono indurre a pensare che i giudizi sulla consonanza siano vaghi e soggettivi; invece, almeno per quanto riguarda le consonanze fondamentali, hanno valore pressoché universale. In qualunque parte del mondo, quando un uomo e un bambino cantano uno stesso motivo, non emettono suoni uguali in altezza, ma ad altezze distinte che tuttavia formano costantemente tra loro un intervallo che noi chiamiamo di ottava.
Quella di ottava non è l'unica consonanza "universale". Se all'interno di tale intervallo si deve trovare un suono centrale, la scelta, nella pressoché totalità dei casi, cadrà su una nota che forma con la nota bassa dell'ottava un intervallo di quinta e, conseguentemente, un intervallo di quarta con la nota alta.
Se prendiamo una corda che produce un determinato suono e desideriamo ottenere il suono superiore di un'ottava, dobbiamo interrompere la corda nel suo punto centrale. Indicando con A la lunghezza della corda che produce il primo suono e con B la lunghezza della sezione che produce il secondo, abbiamo che A: B = 2 :1.
Per salire di una quinta, dobbiamo interrompere la corda ai due terzi e quindi, indicando con C la lunghezza della sezione che produce questo nuovo suono, abbiamo A:C = 3:2. Infine, i suoni prodotti dalle corde C e B formano un intervalli di quarta, e C:B = 4:3. Abbiamo quindi che le tre consonanze principali, ottava quinta e quarta, corrispondono ai rapporti 2:1; 3:2 e 4:3 e possono essere rappresentate impiegando, e in modo "regolare", solo i primi quattro numeri naturali.
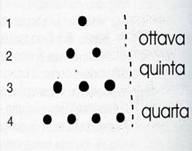
Tale scoperta, che la tradizione attribuisce a Pitagora, ebbe sul pensiero greco un effetto sconvolgente; l'imprevista ma limpidissima corrispondenza tra suoni e numeri, non mediata, come accade per noi, dalla teoria fisica degli armonici, costituì per i Pitagorici il principale argomento a favore della tesi che "tutto è numero".
All'interno della loro scuola fu sancita la quadripartizione della matematica in aritmetica-musica-geometria-astronomia, e la determinazione degli intervalli della scala rimase a lungo il più frequentato campo di applicazione della teoria delle proporzioni.
Rappresentiamo ora la scala composta da quattro suoni in modo logaritmico, essa evidenzia una perfetta simmetria assiale, essendo costituita da due intervalli di quarta (12:9 = 8:6 = 4:3) separati al centro da un intervallo espresso dal rapporto 9:8, che i Greci chiamarono tono (e che esprime la differenza tra una quinta ed una quarta). L'insieme dei quattro numeri 12,9,8, 6 e dei loro reciproci rapporti venne, dai Pitagorici in poi, rappresentato innumerevoli volte, sempre in modo da evidenziare la simmetria; il suo fascino, accresciuto dal fatto che 9 e 8 sono rispettivamente la media aritmetica e la media armonica tra 12 e 6, esercitò a lungo un richiamo molto forte.
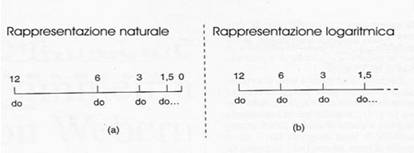
Nicomaco da Gerasa (I secolo d.C) chiamò la quaterna 12-9-8-6 "divina proporzione", per la sintesi perfetta di armonia musicale, rapporti numerici e simmetria spaziale, e fino all'età del temperamento (cioè fino al Settecento) essa rappresentò la base comune a tutte le accordature della scala. Aggiungendo nella parte (b) dello schema una nota all'interno di ciascun intervallo di quarta si hanno complessivamente cinque note diverse, cioè una scala pentatonica, aggiungendone due si ha una scala eptatonica.
Il desiderio di aggiungere tali note in modo da dividere la quarta in due o tre parti uguali tra loro, in modo da ottenere una disposizione simmetrica, si è trovato in conflitto con la simmetria nel significato antico: infatti, poiché uguaglianza di intervalli significa uguaglianza di rapporti, la metà di un intervallo di estremi A e E è espressa dal medio proporzionale, cioè dal punto x tale che A:x = x:E.
Analogamente, dividere un intervallo in N parti uguali significa trovare N medi proporzionali. Ora, un teorema dovuto al pitagorico Archita e riportato nella Sectio Canonis di Euclide asserisce: se A:E = (N+1):N, allora tra A e E non esistono ne uno ne più medi proporzionali (che siano numeri naturali).
Poiché tutte le consonanze finora incontrate -ottava, quinta, quarta - sono espresse da rapporti della forma (N+1):N, il teorema di Archita sancisce l'incompatibilità tra la simmetria nel significato antico e l'equipartizione razionale di intervalli consonanti. In questo rapporto conflittuale, la simmetria nel significato antico ha prevalso incondizionatamente per un periodo che, per la musica occidentale, si è protratto fino al XVIII secolo.
Decisivo in tal senso è stato il sorprendente perdurare della corrispondenza tra consonanze musicali e rapporti della forma (N+1):N anche per le consonanze inferiori a quella di quarta. Infatti la consonanza di terza maggiore (do -mi) e quella di terza minore (mi-sol) sono rispettivamente espresse dai rapporti 5:4 e 6:5. Le note all'interno dell'intervallo di quarta sono state aggiunte in modo da ottenere una di queste due nuove consonanze.
Ma, alla fine del Seicento, si è imposta una soluzione più drastica. Il massimo numero possibile di traslazioni si ottiene se l' ottava è divisa in parti uguali. Essendo l' ottava espressa dal rapporto 2:1, che ha la forma (N+1):N, il Teorema di Archita sancisce l'impossibilità di ottenere una qualunque equipartizione mediante rapporti tra numeri naturali; ed essendo tutte le consonanze espresse da rapporti di questo tipo, una qualunque divisione dell'ottava in parti uguali non potrà contenere al suo interno alcuna consonanza giusta.
Tuttavia, l' orecchio sopporta bene piccoli errori rispetto all'intonazione esatta; confidando su questo fatto, si è scelto di dividere l' ottava in un numero N di parti uguali, scegliendo N in modo tale da poter approssimare soddisfacentemente le note della scala giusta.
Ora, l' ottava ha una ampiezza di circa sei toni (come riporta Euclide nella Sectio Canonis, sei toni determinano un rapporto 531441/262144, di poco superiore a due); ma, avendo l'intervallo di quarta un' ampiezza di circa due toni e mezzo e quello di quinta di circa tre toni e mezzo, per approssimare tali intervalli è necessario disporre di mezzi toni: il numero sei deve essere moltiplicato per due.
Nasce il tal modo la scala temperata, quella dei moderni pianoforti, in cui l'ottava è divisa in dodici intervalli uguali.
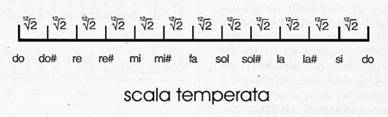
In altre parole, salendo di un tono e scendendo di due semitoni non si ritorna al punto di partenza, e si ottiene invece il cosiddetto comma diatonico o pitagorico, ovvero 1.01316 pari a circa un quarto di semitono temperato, perfettamente percepibile da un orecchio sensibile, soprattutto a frequenza medioalte. L’ orecchio umano, oltre a percepire frequenze comprese tra 16 e 10000 Hertz, limiti oltre i quali si situano gli infrasuoni e gli ultrasuoni, può infatti discriminare intervalli fino a 1/20 di tono. L’ orecchio ha una risposta non lineare, ma logaritmica: alle basse frequenze esso richiede maggiore intensità per percepire un suono, e maggiori intervalli per discriminare suoni indifferenti. Sembra sia stato proprio Pitagora a scoprire il problema del comma, in maniera Empirica. In 7 ottave ci stanno infatti 12 quinte, perche’ un’ ottava contiene 12 semitoni, e una quinta 7: ma diminuendo 7 volte di metà una corda tesa si otteneva un suono distintamente differente da quello ricavato diminuendo 12 volte di un terzo, ikl che significa che salendo il 12 quinte e scendendo di 7 ottave non si ritorna al punto di partenza. La scala Pitagorica con diesis e bemolli richiede dunque 21 note, disposte nel seguente ordiene, dove le varie coppie differiscono di un comma: DO-si bem-re bem-do diesis-RE-mi bem-re diesis-fa bem-MI-FA-mi diesis-sol bem-fa diesis-SOL-la bem-sol diesis-LA-si bem-la diesis-do bem-SI
Gli errori di intonazione delle note temperate rispetto a quelle giuste sono abbastanza contenuti, ed in compenso è possibile qualunque traslazione la cui ampiezza sia multipla del semitono.
La battaglia tra la scala giusta e la scala temperata è stata dunque in parte una battaglia tra la simmetria nel significato antico [ogni intervallo della scala giusta ha la forma (N+1):N] e la simmetria nel significato moderno [qualunque nota della scala temperata, se si prendono ai suoi lati uno stesso numero di note, costituisce un asse di simmetria].
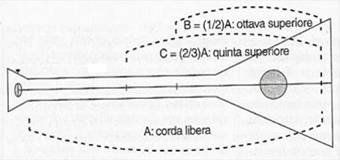
L 'accettazione del temperamento non rappresenta tuttavia il trionfo della seconda sulla prima, bensì il raggiungimento di un compromesso. Del resto, il fatto che la tastiera del pianoforte abbia la sua attuale disposizione testimonia che la scala temperata è un ambiente matematicamente simmetrico disposto, fisicamente, in modo asimmetrico, al fine di potere ben approssimare, con la scala dei tasti bianchi e le sue traslazioni, l' antica simmetria delle proporzioni e delle consonanze.
Il primo tentativo di scala musicale lo si deve al filosofo-matematico Pitagora.
Utilizzando un monocordo e le proprietà delle frazioni (essendo, inoltre, che la sua dottrina prevedeva il numero come "essenza di tutte le cose") costruì la prima scala musicale "teorizzata". essa è però puramente "formale" perché sebbene sia "quadrata" dal punto di vista numerico dei rapporti tra le varie note che la compongono, all'orecchio risulta essere alquanto sgradevole. In effetti, il problema dell' accordatura è così "di base" che sovente non viene neanche rilevato. Eppure le singole note, che troviamo sulla tastiera di un pianoforte così come su quella di un flauto, costituiscono l'alfabeto con cui costruire una qualunque composizione musicale.
La domanda che sorge spontanea è con quale criterio sono stati scelti proprio quei suoni e, soprattutto, come sono state determinate le distanze tra uno e l' altro? In genere, quando si suddivide un intervallo continuo lo si fa con punti equidistanti, e infatti, come attestano vari strumenti musicali antichi, alcuni tentativi si mossero in questa direzione.
Essa tuttavia fu presto abbandonata, perché il criterio che è alla base della scelta dei suoni non è quello spaziale di equidistanza, bensì quello musicale di consonanza. Questo concetto, nei manuali di teoria, è così definito: un intervallo tra due note si dice consonante se, suonando le due note simultaneamente, si ottiene un effetto di gradevolezza e di quiete; si dice invece dissonante se produce un senso di instabilità e di tensione.
I termini impiegati ("gradevolezza", "tensione", "quiete") possono indurre a pensare che i giudizi sulla consonanza siano vaghi e soggettivi; invece, almeno per quanto riguarda le consonanze fondamentali, hanno valore pressoché universale. In qualunque parte del mondo, quando un uomo e un bambino cantano uno stesso motivo, non emettono suoni uguali in altezza, ma ad altezze distinte che tuttavia formano costantemente tra loro un intervallo che noi chiamiamo di ottava.
Quella di ottava non è l'unica consonanza "universale". Se all'interno di tale intervallo si deve trovare un suono centrale, la scelta, nella pressoché totalità dei casi, cadrà su una nota che forma con la nota bassa dell'ottava un intervallo di quinta e, conseguentemente, un intervallo di quarta con la nota alta.
Se prendiamo una corda che produce un determinato suono e desideriamo ottenere il suono superiore di un'ottava, dobbiamo interrompere la corda nel suo punto centrale. Indicando con A la lunghezza della corda che produce il primo suono e con B la lunghezza della sezione che produce il secondo, abbiamo che A: B = 2 :1.
Per salire di una quinta, dobbiamo interrompere la corda ai due terzi e quindi, indicando con C la lunghezza della sezione che produce questo nuovo suono, abbiamo A:C = 3:2. Infine, i suoni prodotti dalle corde C e B formano un intervalli di quarta, e C:B = 4:3. Abbiamo quindi che le tre consonanze principali, ottava quinta e quarta, corrispondono ai rapporti 2:1; 3:2 e 4:3 e possono essere rappresentate impiegando, e in modo "regolare", solo i primi quattro numeri naturali.

Tale scoperta, che la tradizione attribuisce a Pitagora, ebbe sul pensiero greco un effetto sconvolgente; l'imprevista ma limpidissima corrispondenza tra suoni e numeri, non mediata, come accade per noi, dalla teoria fisica degli armonici, costituì per i Pitagorici il principale argomento a favore della tesi che "tutto è numero".
All'interno della loro scuola fu sancita la quadripartizione della matematica in aritmetica-musica-geometria-astronomia, e la determinazione degli intervalli della scala rimase a lungo il più frequentato campo di applicazione della teoria delle proporzioni.
Rappresentiamo ora la scala composta da quattro suoni in modo logaritmico, essa evidenzia una perfetta simmetria assiale, essendo costituita da due intervalli di quarta (12:9 = 8:6 = 4:3) separati al centro da un intervallo espresso dal rapporto 9:8, che i Greci chiamarono tono (e che esprime la differenza tra una quinta ed una quarta). L'insieme dei quattro numeri 12,9,8, 6 e dei loro reciproci rapporti venne, dai Pitagorici in poi, rappresentato innumerevoli volte, sempre in modo da evidenziare la simmetria; il suo fascino, accresciuto dal fatto che 9 e 8 sono rispettivamente la media aritmetica e la media armonica tra 12 e 6, esercitò a lungo un richiamo molto forte.

Nicomaco da Gerasa (I secolo d.C) chiamò la quaterna 12-9-8-6 "divina proporzione", per la sintesi perfetta di armonia musicale, rapporti numerici e simmetria spaziale, e fino all'età del temperamento (cioè fino al Settecento) essa rappresentò la base comune a tutte le accordature della scala. Aggiungendo nella parte (b) dello schema una nota all'interno di ciascun intervallo di quarta si hanno complessivamente cinque note diverse, cioè una scala pentatonica, aggiungendone due si ha una scala eptatonica.
Il desiderio di aggiungere tali note in modo da dividere la quarta in due o tre parti uguali tra loro, in modo da ottenere una disposizione simmetrica, si è trovato in conflitto con la simmetria nel significato antico: infatti, poiché uguaglianza di intervalli significa uguaglianza di rapporti, la metà di un intervallo di estremi A e E è espressa dal medio proporzionale, cioè dal punto x tale che A:x = x:E.
Analogamente, dividere un intervallo in N parti uguali significa trovare N medi proporzionali. Ora, un teorema dovuto al pitagorico Archita e riportato nella Sectio Canonis di Euclide asserisce: se A:E = (N+1):N, allora tra A e E non esistono ne uno ne più medi proporzionali (che siano numeri naturali).
Poiché tutte le consonanze finora incontrate -ottava, quinta, quarta - sono espresse da rapporti della forma (N+1):N, il teorema di Archita sancisce l'incompatibilità tra la simmetria nel significato antico e l'equipartizione razionale di intervalli consonanti. In questo rapporto conflittuale, la simmetria nel significato antico ha prevalso incondizionatamente per un periodo che, per la musica occidentale, si è protratto fino al XVIII secolo.
Decisivo in tal senso è stato il sorprendente perdurare della corrispondenza tra consonanze musicali e rapporti della forma (N+1):N anche per le consonanze inferiori a quella di quarta. Infatti la consonanza di terza maggiore (do -mi) e quella di terza minore (mi-sol) sono rispettivamente espresse dai rapporti 5:4 e 6:5. Le note all'interno dell'intervallo di quarta sono state aggiunte in modo da ottenere una di queste due nuove consonanze.
Ma, alla fine del Seicento, si è imposta una soluzione più drastica. Il massimo numero possibile di traslazioni si ottiene se l' ottava è divisa in parti uguali. Essendo l' ottava espressa dal rapporto 2:1, che ha la forma (N+1):N, il Teorema di Archita sancisce l'impossibilità di ottenere una qualunque equipartizione mediante rapporti tra numeri naturali; ed essendo tutte le consonanze espresse da rapporti di questo tipo, una qualunque divisione dell'ottava in parti uguali non potrà contenere al suo interno alcuna consonanza giusta.
Tuttavia, l' orecchio sopporta bene piccoli errori rispetto all'intonazione esatta; confidando su questo fatto, si è scelto di dividere l' ottava in un numero N di parti uguali, scegliendo N in modo tale da poter approssimare soddisfacentemente le note della scala giusta.
Ora, l' ottava ha una ampiezza di circa sei toni (come riporta Euclide nella Sectio Canonis, sei toni determinano un rapporto 531441/262144, di poco superiore a due); ma, avendo l'intervallo di quarta un' ampiezza di circa due toni e mezzo e quello di quinta di circa tre toni e mezzo, per approssimare tali intervalli è necessario disporre di mezzi toni: il numero sei deve essere moltiplicato per due.
Nasce il tal modo la scala temperata, quella dei moderni pianoforti, in cui l'ottava è divisa in dodici intervalli uguali.

In altre parole, salendo di un tono e scendendo di due semitoni non si ritorna al punto di partenza, e si ottiene invece il cosiddetto comma diatonico o pitagorico, ovvero 1.01316 pari a circa un quarto di semitono temperato, perfettamente percepibile da un orecchio sensibile, soprattutto a frequenza medioalte. L’ orecchio umano, oltre a percepire frequenze comprese tra 16 e 10000 Hertz, limiti oltre i quali si situano gli infrasuoni e gli ultrasuoni, può infatti discriminare intervalli fino a 1/20 di tono. L’ orecchio ha una risposta non lineare, ma logaritmica: alle basse frequenze esso richiede maggiore intensità per percepire un suono, e maggiori intervalli per discriminare suoni indifferenti. Sembra sia stato proprio Pitagora a scoprire il problema del comma, in maniera Empirica. In 7 ottave ci stanno infatti 12 quinte, perche’ un’ ottava contiene 12 semitoni, e una quinta 7: ma diminuendo 7 volte di metà una corda tesa si otteneva un suono distintamente differente da quello ricavato diminuendo 12 volte di un terzo, ikl che significa che salendo il 12 quinte e scendendo di 7 ottave non si ritorna al punto di partenza. La scala Pitagorica con diesis e bemolli richiede dunque 21 note, disposte nel seguente ordiene, dove le varie coppie differiscono di un comma: DO-si bem-re bem-do diesis-RE-mi bem-re diesis-fa bem-MI-FA-mi diesis-sol bem-fa diesis-SOL-la bem-sol diesis-LA-si bem-la diesis-do bem-SI
Gli errori di intonazione delle note temperate rispetto a quelle giuste sono abbastanza contenuti, ed in compenso è possibile qualunque traslazione la cui ampiezza sia multipla del semitono.
La battaglia tra la scala giusta e la scala temperata è stata dunque in parte una battaglia tra la simmetria nel significato antico [ogni intervallo della scala giusta ha la forma (N+1):N] e la simmetria nel significato moderno [qualunque nota della scala temperata, se si prendono ai suoi lati uno stesso numero di note, costituisce un asse di simmetria].

L 'accettazione del temperamento non rappresenta tuttavia il trionfo della seconda sulla prima, bensì il raggiungimento di un compromesso. Del resto, il fatto che la tastiera del pianoforte abbia la sua attuale disposizione testimonia che la scala temperata è un ambiente matematicamente simmetrico disposto, fisicamente, in modo asimmetrico, al fine di potere ben approssimare, con la scala dei tasti bianchi e le sue traslazioni, l' antica simmetria delle proporzioni e delle consonanze.