Riconoscimento delle caratteristiche di una funzione attraverso l'esame della sua rappresentazione grafica, e nota la sua equazione.
campo di esistenza | intersezione assi | asintoti | monotonia | massimi e minimi
Nella figura è rappresentata la funzione goniometrica 
.
Poiché la funzione è periodica di periodo 
, restringi lo studio all'intervallo 
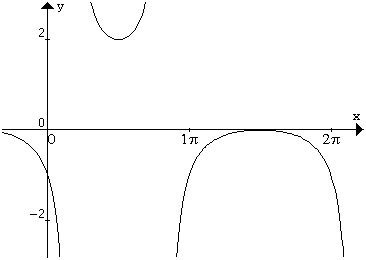
1. Considerato lintervallo di periodicità 
, quale tra gli insiemi proposti è il suo CdE?
d)nessuno dei precedenti
2. Calcola le intersezioni della curva con gli assi coordinati e rispondi:
a)la curva interseca l'asse x nel punto 
e non interseca l'asse y
b)la curva interseca l'asse x nel punto e l'asse y nel punto (0;-1)
c)la curva interseca l'asse x nel punto 
e l'asse y nel punto (0;-1)
d)nessuno dei precedenti
3. Stabilisci se la curva presenta degli asintoti nell'intervallo :
a)la retta 
è l'unico asintoto verticale della curva
b)la retta 
è l'unico asintoto verticale della curva
c)le rette e sono due asintoti verticali della curva
d)la funzione non presenta asintoti verticali
4. Stabilisci se e in quali intervalli la funzione è decrescente:
a)in 
la funzione è decrescente
b)in 
e in 
la funzione è decrescente
c)in 
la funzione è decrescente
d)la funzione è sempre crescente
5. Quali tra le seguenti affermazioni ritieni corretta:
a)
minimo relativo; 
massimo relativo; 
punto di flesso
b) minimo relativo; nessun massimo relativo; 
punto di flesso
c) minimo relativo; massimo relativo; non ci sono punti di flesso
d)nessuna delle precedenti
