ACUSTICA
MUSICALE
Quando ascoltiamo una traccia musicale di qualsiasi genere sentiamo un "ritmo".
Il "ritmo" è un fenomeno musicale periodico ovvero, dopo certi intervalli costanti, riprende dalla posizione di partenza.
La percezione del ritmo avviene grazie a degli accenti che lo compongono e che ci fanno avvertire una successione di fasi regolata e precisa: inizio, decorso, fine.
Questi accenti dettano il cosiddetto "battere-levare" che regola il tempo in musica.
Prendiamo un metronomo, o un orologio fa lo stesso; ad ogni battere della lancetta noi avvertiamo un accento che è il battere.
Ebbene il levare è l’accento che "non c’è" nel senso che è l’accento che vi è tra due "battere"; la successione ottenuta sarà battere – levare – battere, forte –debole – forte.
Oltre al ritmo nella musica vi sono le note.
La sequenza ordinata di note produce la melodia di un brano, ma per far sì che una melodia abbia senso bisogna dare alle note una durata ed inscriverle in un pentagramma in modo da dare dei canoni. L’unità in musica è il 4/4.

Ma un brano costituito da sole note è troppo "pieno", ecco perciò la necessità delle pause.
Le pause sono di molti tipi e ognuna corrisponde ad una figura metrica.

Si deve correggere l’affermazione precedente riguardo il 4/4, poiché esso fa sì che in una battuta la somma delle durate e delle pause dia l’unità.
Oltre alla durata e al ritmo vi è l’importanza delle note.
Le note sono 7, 12 se contiamo le relative alterazioni.
Si dice "tono" la nota semplice e "semitono" la sua alterazione.
Toni e semitoni derivano da precisi rapporti matematici tra le parti di una corda.
Questo deriva da un esperimento di Pitagora.
Prendendo una corda che, vibrando, produce un suono, ipotizziamo un Do; Pitagora dimostrò che se divisa in due parti uguali, e fatta vibrare, il suono della corda sarà, si un Do, ma di un’ottava sopra, il Do2.
Se sfiorata in altre parti della sua lunghezza , il fenomeno si ripeterà ma ne scaturiranno suoni sempre più acuti.
Sfiorata ad 1/3 del totale si otterrà la dodicesima nota Sol2 (o 3° armonico).
Sfiorata ad 1/4 si otterrà la doppia ottava: Do3 (o 4° armonico).
Sfiorata ad 1/5 si otterrà la diciassettesima nota: Mi3 (o 5° armonico).
Ecc….

Dalle relazioni precedenti si possono ottenere i rapporti che intercorrono fra 2 suoni a distanza di un qualsiasi intervallo servendoci dei numeri d’ordine della serie armonica.

Dai rapporti che intercorrono fra le parti della corda pizzicata, Pitagora formò una scala basata sul rapporto fra un suono, la sua quinta e la sua ottava.
Egli stabilì che, se si fa vibrare una corda 1/2, il suono ottenuto sarà in rapporto con quello originale pari a 2:1.
I 2/3 di una corda la quinta mentre i 3/4 danno una quarta; così che il rapporto di 2 suoni alla quinta è 3:2, quella di due suoni alla quarta come 4:3.
Procedendo di quinta in quinta, Pitagora calcolò l’altezza di tutti i suoni.


La nota Fa che manca si ottiene con il procedimento inverso, ovvero ponendo prima del Do la sua quinta.
I suoni ottenuti si coordinano in un’ottava, aumentando il Fa di un’ottava, diminuendo il Re e il La di un’ottava e Mi e Si di due, modificando i rapporti moltiplicando per 2 e dividendo per 2 o per 4.
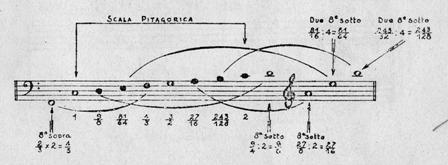
Questa è la scala pitagorica e venne utilizzata fino al ‘500 quando cominciò a farsi strada la polifonia vocale. Allora questa scala non era adatta al tipo di musica e perciò si adattò il modello alle necessità ottenendo la scala naturale.
Questa scala ha la particolarità di avere l’intonazione dei gradi, rispetto alla tonica, determinati dai rapporti derivati dal fenomeno dei suoni "armonici".
Basandoci su questi, calcoliamo il rapporto fra i suoni che compongono una scala maggiore e la tonica della stessa scala.

ciascun suono della stessa scala con il suono subito prima, dividendo il rapporto del suono superiore per quello del suono inferiore.
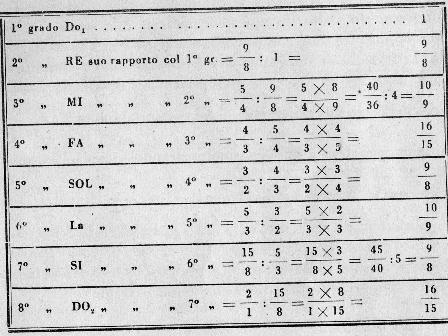
Si ottengono tre specie di intervalli:
1) uno di 9/8 (fra Do-Re; Fa-Sol; La-Si) detto "tono maggiore";
2) uno di 10/9 (fra Re-Mi; Sol-La) detto "tono minore";
3) uno di 16/15 (fra Mi-Fa; Si-Do) detto "semitono diatonico".
Confrontando il tono maggiore e il tono minore si vedrà che la differenza è:
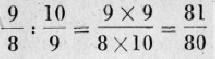
Tale differenza è chiamata "comma".
Confrontando il tono minore con il semitono diatonico avremo:
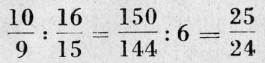
Questa differenza si chiama "semitono cromatico" ed esprime la differenza che passa tra una nota naturale e la stessa "diesizzata"; oppure tra una nota "bemollizzata" e la stessa naturale.
Si rileva che si può aumentare ( diesizzandola) o diminuire (bemollizzando) una nota moltiplicando o dividendo il numero delle sue vibrazioni per 25/24.
Es:
Re di 9/8 vibrazioni si eleva a Re # per: 9/8 x 25/24
Re di 9/8 vibrazioni si abbassa a Re b per: 9/8 : 25/24
Ma con l’aumento d’uso degli strumenti a tastiera o a suono fisso (come organo, clavicordo e clavicembalo), la scala naturale venne sostituita dalla scala temperata.
Questa scala è basata sulla divisione dell’ottava in 12 semitoni uguali (per valore).
Scompaiono così i toni maggiori, minori e i comma ed il semitono cominciò a rappresentare la metà esatta del tono.
Mediante ciò gli intervalli avevano sempre lo stesso valore in qualsiasi tonalità.
Questa scala agevolò la tecnica strumentale e la costruzione di strumenti a tastiera.
Per accordare i 12 suoni di un’ottava e per stabilire l’intervallo costante tra una nota della gamma temperata e la nota precedente, è stato trovato un numero che rappresenta esattamente la dodicesima parte della differenza che passa fra uno e due (ovvero tra una nota e la sua ottava).
Questo numero è la radice dodicesima di 2, ovvero 1,05946.
Moltiplicando il numero di vibrazioni di un dato suono per 1,05946 si ottiene il semitono superiore, mentre dividendo per lo stesso numero si otterrà il semitono inferiore.
Es:
Il La del diapason ha 870 vibrazioni, per sapere le vibrazioni del La # e del La b si dovrà fare:
La #: 870 x 1,05946 = 921,73
La b: 870 : 1,05946 = 821
Per calcolare le vibrazioni di altri suoni, più distanti di un semitono dal suono base, bisognerà:
1) calcolare quanti semitoni vi sono tra i due suoni;
2) elevare 1,05946 a potenza con esponente pari al numero di semitoni contati prima
3) moltiplicare/dividere le vibrazioni del suono base per il numero ottenuto.
ALTRI TIPI DI SCALE TEMPERATE
Teniamo presente che, nella scala temperata classica (divisione dell’ottava in 12 semitoni), il semitono ha frequenza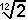 proprio
per il numero di semitoni. Il radicando è la frequenza dell’ottava, e
quindi non muta se la dividiamo, per esempio, in 11 parti anziché in 12. Quello
che cambia è l’indice della radice: dividendo DO1-DO2 in n intervalli il
più piccolo di essi ha frequenza
proprio
per il numero di semitoni. Il radicando è la frequenza dell’ottava, e
quindi non muta se la dividiamo, per esempio, in 11 parti anziché in 12. Quello
che cambia è l’indice della radice: dividendo DO1-DO2 in n intervalli il
più piccolo di essi ha frequenza
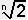 .
.
Nella tabella seguente sono indicati nella colonna di sinistra il valore di n (da 1 fino a 24), e in quella di destra le frequenze delle varie note (che, ovviamente, sono n+1). Sono indicate rispettivamente in rosso e in verde le note che approssimano MI1 (5/4) e SOL1 (3/2) della scala naturale con un errore minore dell’1%. Come si può facilmente verificare, tra i casi considerati solo una divisione dell’ottava in 12, 19 o 24 parti permette di ottenere un accordo abbastanza somigliante a quello di do maggiore della scala naturale (DO1-MI1-SOL1), nel senso che l’errore che si commette è minore in entrambi i casi dell’1%.
Un accordo ricavato, lo ricordiamo, proprio dal fenomeno fisico dei suoni armonici, e per questo riconosciuto come gradevole dall’orecchio. Certo nulla vieta (o avrebbe vietato) di utilizzare scale meno immediate: è stato adottato il temperamento con 12 semitoni non perché non potesse accadere diversamente, ma perché la storia della musica occidentale ha seguito (almeno fino alla prima metà del 1900) una delle strade più semplici tra le tante possibili.

NUMERO DI INTERVALLI IN CUI VIENE DIVISA L’OTTAVA (COLONNA DI SINISTRA) E FREQUENZE DELLE NOTE (A DESTRA). I COLORI ROSSO E VERDE INDICANO QUELLE CHE APPROSSIMANO RISPETTIVAMENTE MI E SOL DELLA SCALA NATURALE CON UN ERRORE INFERIORE ALL’1%
Avrebbe dato comunque un effetto altrettanto gradevole non solo una divisione in 24 parti (basterebbe dividere ogni semitono in due quarti di tono uguali, visto che 24 è il doppio di 12), ma anche in 19. Ecco come potrebbe essere la tastiera di un pianoforte che utilizzi questa scala: due tasti neri tra due bianchi, tranne nel caso di mi-fa e si-do, dove ce n’è uno solo. In altre parole, chiamando tono l’intervallo che c’è, per esempio, tra do1 e re1 (ma il termine assume un significato diverso rispetto al temperamento classico), ogni tono viene diviso in tre parti uguali; inoltre tra mi e fa e tra si e do c’è un intervallo di due terzi di tono. La scala cromatica diventa formata da do, do#, reb, re, re#, mib, mi, mi#, fa, fa#, solb, sol, sol#, lab, la, la#, sib, si, si#, do. Come si può notare, ho chiamato do# e reb le note che si ottengono rispettivamente innalzando do e abbassando re di un terzo di tono: a differenza di quanto accade dividendo l’ottava in 12 parti, non si tratta della stessa nota.
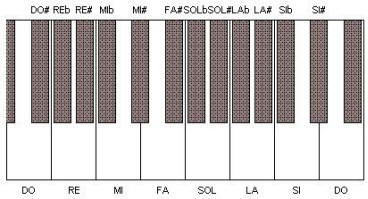
COSÌ POTREBBE ESSERE LA TASTIERA DI UN PIANOFORTE SE L’OTTAVA VENISSE DIVISA IN 19 INTERVALLI UGUALI
Se ci limitiamo alle note corrispondenti ai tasti bianchi di questo ipotetico pianoforte, non c’è una grande differenza con la scala temperata classica, come possiamo verificare dalla tabella seguente.
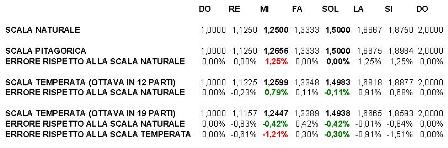
FREQUENZE DELLE VARIE SCALE ED ERRORI RISPETTO A QUELLE NATURALE E TEMPERATA CLASSICA
Si possono ora scaricare vari esempi musicali, da cui si evince che sia la scala di do maggiore, sia la melodia di Fra Martino non sono molto diverse se si divide l’ottava in 19 anziché in 12 parti. Infine, possiamo ascoltare una melodia ed una sua variazione basate rispettivamente sulla divisione in 12 e in 19 intervalli. Anche in questo caso l’effetto non è poi così poco familiare come ci si potrebbe attendere.
In definitiva una scala temperata con 19 intervalli uguali tra due do consecutivi non sembra particolarmente strana perché il nostro orecchio riconosce l’accordo di do maggiore che abbiamo ricavato dai suoni armonici, e che, pur non essendo esatto, non se ne distanzia poi molto.
Quando ascoltiamo una traccia musicale di qualsiasi genere sentiamo un "ritmo".
Il "ritmo" è un fenomeno musicale periodico ovvero, dopo certi intervalli costanti, riprende dalla posizione di partenza.
La percezione del ritmo avviene grazie a degli accenti che lo compongono e che ci fanno avvertire una successione di fasi regolata e precisa: inizio, decorso, fine.
Questi accenti dettano il cosiddetto "battere-levare" che regola il tempo in musica.
Prendiamo un metronomo, o un orologio fa lo stesso; ad ogni battere della lancetta noi avvertiamo un accento che è il battere.
Ebbene il levare è l’accento che "non c’è" nel senso che è l’accento che vi è tra due "battere"; la successione ottenuta sarà battere – levare – battere, forte –debole – forte.
Oltre al ritmo nella musica vi sono le note.
La sequenza ordinata di note produce la melodia di un brano, ma per far sì che una melodia abbia senso bisogna dare alle note una durata ed inscriverle in un pentagramma in modo da dare dei canoni. L’unità in musica è il 4/4.

Ma un brano costituito da sole note è troppo "pieno", ecco perciò la necessità delle pause.
Le pause sono di molti tipi e ognuna corrisponde ad una figura metrica.

Si deve correggere l’affermazione precedente riguardo il 4/4, poiché esso fa sì che in una battuta la somma delle durate e delle pause dia l’unità.
Oltre alla durata e al ritmo vi è l’importanza delle note.
Le note sono 7, 12 se contiamo le relative alterazioni.
Si dice "tono" la nota semplice e "semitono" la sua alterazione.
Toni e semitoni derivano da precisi rapporti matematici tra le parti di una corda.
Questo deriva da un esperimento di Pitagora.
Prendendo una corda che, vibrando, produce un suono, ipotizziamo un Do; Pitagora dimostrò che se divisa in due parti uguali, e fatta vibrare, il suono della corda sarà, si un Do, ma di un’ottava sopra, il Do2.
Se sfiorata in altre parti della sua lunghezza , il fenomeno si ripeterà ma ne scaturiranno suoni sempre più acuti.
Sfiorata ad 1/3 del totale si otterrà la dodicesima nota Sol2 (o 3° armonico).
Sfiorata ad 1/4 si otterrà la doppia ottava: Do3 (o 4° armonico).
Sfiorata ad 1/5 si otterrà la diciassettesima nota: Mi3 (o 5° armonico).
Ecc….

Dalle relazioni precedenti si possono ottenere i rapporti che intercorrono fra 2 suoni a distanza di un qualsiasi intervallo servendoci dei numeri d’ordine della serie armonica.

Dai rapporti che intercorrono fra le parti della corda pizzicata, Pitagora formò una scala basata sul rapporto fra un suono, la sua quinta e la sua ottava.
Egli stabilì che, se si fa vibrare una corda 1/2, il suono ottenuto sarà in rapporto con quello originale pari a 2:1.
I 2/3 di una corda la quinta mentre i 3/4 danno una quarta; così che il rapporto di 2 suoni alla quinta è 3:2, quella di due suoni alla quarta come 4:3.
Procedendo di quinta in quinta, Pitagora calcolò l’altezza di tutti i suoni.


La nota Fa che manca si ottiene con il procedimento inverso, ovvero ponendo prima del Do la sua quinta.
I suoni ottenuti si coordinano in un’ottava, aumentando il Fa di un’ottava, diminuendo il Re e il La di un’ottava e Mi e Si di due, modificando i rapporti moltiplicando per 2 e dividendo per 2 o per 4.

Questa è la scala pitagorica e venne utilizzata fino al ‘500 quando cominciò a farsi strada la polifonia vocale. Allora questa scala non era adatta al tipo di musica e perciò si adattò il modello alle necessità ottenendo la scala naturale.
Questa scala ha la particolarità di avere l’intonazione dei gradi, rispetto alla tonica, determinati dai rapporti derivati dal fenomeno dei suoni "armonici".
Basandoci su questi, calcoliamo il rapporto fra i suoni che compongono una scala maggiore e la tonica della stessa scala.

ciascun suono della stessa scala con il suono subito prima, dividendo il rapporto del suono superiore per quello del suono inferiore.

Si ottengono tre specie di intervalli:
1) uno di 9/8 (fra Do-Re; Fa-Sol; La-Si) detto "tono maggiore";
2) uno di 10/9 (fra Re-Mi; Sol-La) detto "tono minore";
3) uno di 16/15 (fra Mi-Fa; Si-Do) detto "semitono diatonico".
Confrontando il tono maggiore e il tono minore si vedrà che la differenza è:
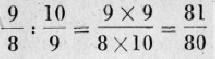
Tale differenza è chiamata "comma".
Confrontando il tono minore con il semitono diatonico avremo:
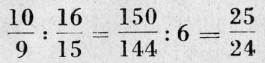
Questa differenza si chiama "semitono cromatico" ed esprime la differenza che passa tra una nota naturale e la stessa "diesizzata"; oppure tra una nota "bemollizzata" e la stessa naturale.
Si rileva che si può aumentare ( diesizzandola) o diminuire (bemollizzando) una nota moltiplicando o dividendo il numero delle sue vibrazioni per 25/24.
Es:
Re di 9/8 vibrazioni si eleva a Re # per: 9/8 x 25/24
Re di 9/8 vibrazioni si abbassa a Re b per: 9/8 : 25/24
Ma con l’aumento d’uso degli strumenti a tastiera o a suono fisso (come organo, clavicordo e clavicembalo), la scala naturale venne sostituita dalla scala temperata.
Questa scala è basata sulla divisione dell’ottava in 12 semitoni uguali (per valore).
Scompaiono così i toni maggiori, minori e i comma ed il semitono cominciò a rappresentare la metà esatta del tono.
Mediante ciò gli intervalli avevano sempre lo stesso valore in qualsiasi tonalità.
Questa scala agevolò la tecnica strumentale e la costruzione di strumenti a tastiera.
Per accordare i 12 suoni di un’ottava e per stabilire l’intervallo costante tra una nota della gamma temperata e la nota precedente, è stato trovato un numero che rappresenta esattamente la dodicesima parte della differenza che passa fra uno e due (ovvero tra una nota e la sua ottava).
Questo numero è la radice dodicesima di 2, ovvero 1,05946.
Moltiplicando il numero di vibrazioni di un dato suono per 1,05946 si ottiene il semitono superiore, mentre dividendo per lo stesso numero si otterrà il semitono inferiore.
Es:
Il La del diapason ha 870 vibrazioni, per sapere le vibrazioni del La # e del La b si dovrà fare:
La #: 870 x 1,05946 = 921,73
La b: 870 : 1,05946 = 821
Per calcolare le vibrazioni di altri suoni, più distanti di un semitono dal suono base, bisognerà:
1) calcolare quanti semitoni vi sono tra i due suoni;
2) elevare 1,05946 a potenza con esponente pari al numero di semitoni contati prima
3) moltiplicare/dividere le vibrazioni del suono base per il numero ottenuto.
ALTRI TIPI DI SCALE TEMPERATE
Teniamo presente che, nella scala temperata classica (divisione dell’ottava in 12 semitoni), il semitono ha frequenza
Nella tabella seguente sono indicati nella colonna di sinistra il valore di n (da 1 fino a 24), e in quella di destra le frequenze delle varie note (che, ovviamente, sono n+1). Sono indicate rispettivamente in rosso e in verde le note che approssimano MI1 (5/4) e SOL1 (3/2) della scala naturale con un errore minore dell’1%. Come si può facilmente verificare, tra i casi considerati solo una divisione dell’ottava in 12, 19 o 24 parti permette di ottenere un accordo abbastanza somigliante a quello di do maggiore della scala naturale (DO1-MI1-SOL1), nel senso che l’errore che si commette è minore in entrambi i casi dell’1%.
Un accordo ricavato, lo ricordiamo, proprio dal fenomeno fisico dei suoni armonici, e per questo riconosciuto come gradevole dall’orecchio. Certo nulla vieta (o avrebbe vietato) di utilizzare scale meno immediate: è stato adottato il temperamento con 12 semitoni non perché non potesse accadere diversamente, ma perché la storia della musica occidentale ha seguito (almeno fino alla prima metà del 1900) una delle strade più semplici tra le tante possibili.

NUMERO DI INTERVALLI IN CUI VIENE DIVISA L’OTTAVA (COLONNA DI SINISTRA) E FREQUENZE DELLE NOTE (A DESTRA). I COLORI ROSSO E VERDE INDICANO QUELLE CHE APPROSSIMANO RISPETTIVAMENTE MI E SOL DELLA SCALA NATURALE CON UN ERRORE INFERIORE ALL’1%
Avrebbe dato comunque un effetto altrettanto gradevole non solo una divisione in 24 parti (basterebbe dividere ogni semitono in due quarti di tono uguali, visto che 24 è il doppio di 12), ma anche in 19. Ecco come potrebbe essere la tastiera di un pianoforte che utilizzi questa scala: due tasti neri tra due bianchi, tranne nel caso di mi-fa e si-do, dove ce n’è uno solo. In altre parole, chiamando tono l’intervallo che c’è, per esempio, tra do1 e re1 (ma il termine assume un significato diverso rispetto al temperamento classico), ogni tono viene diviso in tre parti uguali; inoltre tra mi e fa e tra si e do c’è un intervallo di due terzi di tono. La scala cromatica diventa formata da do, do#, reb, re, re#, mib, mi, mi#, fa, fa#, solb, sol, sol#, lab, la, la#, sib, si, si#, do. Come si può notare, ho chiamato do# e reb le note che si ottengono rispettivamente innalzando do e abbassando re di un terzo di tono: a differenza di quanto accade dividendo l’ottava in 12 parti, non si tratta della stessa nota.

COSÌ POTREBBE ESSERE LA TASTIERA DI UN PIANOFORTE SE L’OTTAVA VENISSE DIVISA IN 19 INTERVALLI UGUALI
Se ci limitiamo alle note corrispondenti ai tasti bianchi di questo ipotetico pianoforte, non c’è una grande differenza con la scala temperata classica, come possiamo verificare dalla tabella seguente.

FREQUENZE DELLE VARIE SCALE ED ERRORI RISPETTO A QUELLE NATURALE E TEMPERATA CLASSICA
Si possono ora scaricare vari esempi musicali, da cui si evince che sia la scala di do maggiore, sia la melodia di Fra Martino non sono molto diverse se si divide l’ottava in 19 anziché in 12 parti. Infine, possiamo ascoltare una melodia ed una sua variazione basate rispettivamente sulla divisione in 12 e in 19 intervalli. Anche in questo caso l’effetto non è poi così poco familiare come ci si potrebbe attendere.
In definitiva una scala temperata con 19 intervalli uguali tra due do consecutivi non sembra particolarmente strana perché il nostro orecchio riconosce l’accordo di do maggiore che abbiamo ricavato dai suoni armonici, e che, pur non essendo esatto, non se ne distanzia poi molto.