|
 Una funzione f tra due insiemi non vuoti A e B è una regola che associa ad ogni elemento di A un unico elemento di B. Una funzione f tra due insiemi non vuoti A e B è una regola che associa ad ogni elemento di A un unico elemento di B.
Indichiamo questa corrispondenza tra insiemi: 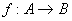 . .
 Una funzione Una funzione 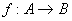 , A e B sottoinsiemi di R, si dice matematica o analitica se esiste una relazione y = f(x) che permette di calcolare univocamente il corrispondente valore y appartenente a B. , A e B sottoinsiemi di R, si dice matematica o analitica se esiste una relazione y = f(x) che permette di calcolare univocamente il corrispondente valore y appartenente a B.
 Questa corrispondenza tra elementi si indica con: y = f(x) (si legge effe di x). Questa corrispondenza tra elementi si indica con: y = f(x) (si legge effe di x).
Lequazione y = f(x) è lespressione analitica della funzione matematica, con x e y rispettivamente variabile indipendente e variabile dipendente.
 Se x è un qualsiasi elemento dellinsieme A ( Se x è un qualsiasi elemento dellinsieme A (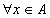 ) con f (x) indichiamo lelemento ) con f (x) indichiamo lelemento 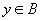 che corrisponde ad x mediante la funzione f . che corrisponde ad x mediante la funzione f .
Lelemento y di B si dice immagine di x mediante f.
 Il dominio D (o Campo di Esistenza CdE, o anche insieme di definizione) di una funzione è il più ampio sottoinsieme di R costituito da tutti e soli i valori della x per cui esistano finiti i corrispondenti valori di y = f(x). Il dominio D (o Campo di Esistenza CdE, o anche insieme di definizione) di una funzione è il più ampio sottoinsieme di R costituito da tutti e soli i valori della x per cui esistano finiti i corrispondenti valori di y = f(x).
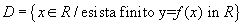
 Il codominio C di una funzione è il sottoinsieme di R costituito da tutti gli elementi y corrispondenti dei punti x appartenenti al dominio della funzione. Il codominio C di una funzione è il sottoinsieme di R costituito da tutti gli elementi y corrispondenti dei punti x appartenenti al dominio della funzione.
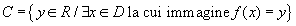
 Una funzione f si dice numerica o aritmetica se il suo dominio è in N ed è a valori in N. Una funzione f si dice numerica o aritmetica se il suo dominio è in N ed è a valori in N. 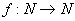
|