|
Sequenza dei passi utili allo studio
di una funzione reale
|
In pratica
|
|
Stabilire se la funzione presenta delle simmetrie e/o è periodica.
|
» Se 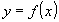 è simmetrica
rispetto allasse y, deve verificarsi: è simmetrica
rispetto allasse y, deve verificarsi:
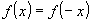 . (funzione pari) . (funzione pari)
» Se 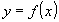 è simmetrica rispetto allorigine degli assi, deve verificarsi:
è simmetrica rispetto allorigine degli assi, deve verificarsi:
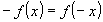 . (funzione dispari) . (funzione dispari)
Nel caso in cui la funzione sia simmetrica, si può restringere lo studio della
funzione ai soli valori positivi e dunque costruire il grafico nel solo semipiano 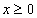 ;
per ottenere il grafico completo basterà simmetrizzare la curva ottenuta rispetto allasse y o allOrigine. ;
per ottenere il grafico completo basterà simmetrizzare la curva ottenuta rispetto allasse y o allOrigine.
» Se 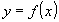 è periodica, si può limitare lo studio allampiezza del periodo.
è periodica, si può limitare lo studio allampiezza del periodo.
|
|
Determinare il Campo di Esistenza, o Dominio, della funzione.
(Si tratta di individuare gli intervalli in cui la funzione assume valori Reali;
ovvero determinare linsieme dei punti 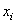 in
cui la funzione non è definita ed escluderli). in
cui la funzione non è definita ed escluderli).
|
Classifica il tipo di funzione:
» se è una
funzione razionale intera il suo dominio è costituito da tutto
lasse Reale
» se
la funzione è una razionale fratta, imponi che il denominatore
sia diverso da zero.
I punti che annullano il denominatore della funzione non appartengono al suo
CDE, per tali punti 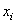 la
funzione non esiste; le rette verticali passanti per quei punti sono asintoti
verticali per la curva; la
funzione non esiste; le rette verticali passanti per quei punti sono asintoti
verticali per la curva;
» se
la funzione è irrazionale, guarda lindice del radicale:
» se è pari
dovrai imporre che il radicando non sia negativo poiché la funzione è a
valori Reali,
» se è dispari,
non ci sono imposizioni.
» Se
la funzione è logaritmica ricordati di imporre che largomento
del logaritmo sia strettamente positivo.
» Se
la funzione è esponenziale non ci sono imposizioni.
» Se
la funzione è trigonometrica bisognerà imporre che gli argomenti
della funzione tangente siano diversi da multipli dispari di
angoli retti 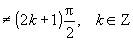 . .
» Quando
la funzione è composta da funzioni di tipo diverso tutte le imposizioni
dovranno essere verificate contemporaneamente, ovvero le condizioni
dovranno essere legate e condotte algebricamente come un sistema
di equazioni.
Scrivi il dominio come UNIONE dei diversi intervalli in cui la
funzione assume valori Reali.
Segna graficamente gli intervalli o i punti in cui la funzione
non esiste.
|
|
Studiare con i limiti il comportamento della funzione agli estremi
del CDE.
|
Calcola i limiti, sinistro e destro, della funzione nellintorno
dei punti 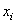
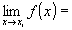 ...... ......
e allinfinito
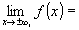 ...... ......
Riporta con un segno grafico il comportamento della curva nellintorno di tali
punti.
|
|
Ricerca degli eventuali asintoti verticali e orizzontali
|
Calcola i limiti:
» Se 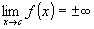 , ,
allora 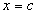 è un asintoto verticale. è un asintoto verticale.
» Se 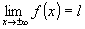 (finito)
, (finito)
,
allora 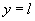 è un asintoto orizzontale è un asintoto orizzontale
|
|
Ricercare leventuale intersezione della funzione con lasse x
|
Poni a sistema lequazione della curva con lequazione dellasse
delle ascisse:
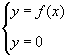
ovvero risolvi lequazione 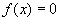 . .
|
|
Ricercare leventuale intersezione della funzione con lasse y
|
Poni a sistema lequazione della curva con lequazione dellasse delle ordinate:
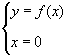
ovvero calcola 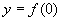 . .
|
|
Studiare il segno della funzione
|
Studia la disequazione 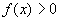 . .
Negli intervalli in cui la funzione risulta positiva, la curva sarà situata sopra
lasse delle ascisse.
Riporta i risultati sul grafico, escludendo le zone che la curva non attraversa.
|
|
Calcolo delle derivate prima e seconda.
Il calcolo della derivata prima serve per determinare gli intervalli in cui la
funzione cresce o descresce, e per individuare i probabili punti di massimo e
minimo relativi.
Il calcolo della derivata seconda serve per determinare gli intervalli in cui
la curva è concava o convessa, e per individuare i probabili punti di flesso.
|
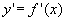 =
.............. =
..............
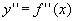 =
.............. =
..............
|
|
Ricerca degli eventuali punti di massimo e di minimo relativo.
|
C.N. affinché un punto sia di massimo o di minimo relativo è che 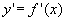 =
0. =
0.
Dunque si tratta di risolvere tale equazione. I valori 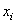 che
la soddisfano sono solo probabili punti di massimo o minimo relativi, in quanto
potrebbero anche essere punti di flesso. che
la soddisfano sono solo probabili punti di massimo o minimo relativi, in quanto
potrebbero anche essere punti di flesso.
I punti in cui si annulla la derivata prima si dicono punti stazionari o punti
critici.
|
|
Studio della monotonia della funzione
|
Per sapere se questi sono punti di massimo o di minimo per la
curva si può procedere in due modi.
1° metodo: si studia il segno della derivata prima, ovvero
si impone che 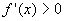 . .
Lo studio degli intervalli di monotonia, cioè dove la curva è crescente o decrescente,
ci fa comprendere se i punti trovati sono di massimo o di minimo.
Se la derivata nellintorno di tali punti non cambia di segno, questi non sono
né di massimo né di minimo.
2° metodo: si sostituiscono le ascisse dei punti 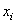 nella
derivata seconda e si guarda il segno che questa assume. nella
derivata seconda e si guarda il segno che questa assume.
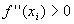 :
se è positiva, la concavità sarà rivolta verso lalto perciò il
punto è di minimo; :
se è positiva, la concavità sarà rivolta verso lalto perciò il
punto è di minimo;
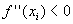 :
se è negativa, la concavità sarà rivolta verso il basso per cui
il punto è un massimo. :
se è negativa, la concavità sarà rivolta verso il basso per cui
il punto è un massimo.
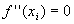 :
se è nulla, il punto è molto probabilmente un flesso. :
se è nulla, il punto è molto probabilmente un flesso.
|
|
Calcolo delle ordinate degli eventuali punti di massimo e di minimo
relativo
|
Sostituisci una alla volta le ascisse dei punti di massimo o di
minimo nellequazione della curva e ricava lordinata.
Riporta con un segno i risultati sul grafico.
|
|
Studio dei punti di non derivabiltà
|
Determina il Campo di Esistenza della derivata prima 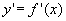 . .
Se 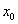 è un punto appartenente al CDE della funzione, ma è un punto di non
derivabilità:
è un punto appartenente al CDE della funzione, ma è un punto di non
derivabilità:
» se 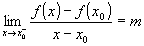 e e 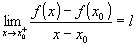 con con 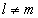 , ,
allora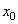 è un punto angoloso;
è un punto angoloso;
» se 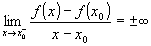 e e 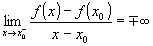 , ,
allora 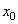 è una cuspide
è una cuspide
» se 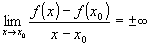 , ,
allora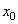 è un flesso a tangente verticale.
è un flesso a tangente verticale.
|
|
Ricerca degli eventuali punti di flesso a tangente orizzontale
|
Imponi 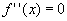 e
risolvi. e
risolvi.
I valori che soddisfano lequazione sono molto probabilmente le ascisse dei punti
di flesso.
|
|
Studio della concavità e della convessità della funzione
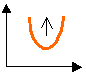
convessa |
concava |
|
Studia il segno della derivata seconda: 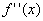 > 0. > 0.
Negli intervalli in cui risulta positiva (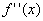 > 0),
la curva rivolge la concavità verso l'alto (convessa), in caso contrario ( > 0),
la curva rivolge la concavità verso l'alto (convessa), in caso contrario (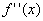 < 0)
la concavità si volge verso il basso (concava). < 0)
la concavità si volge verso il basso (concava).
Le soluzioni di 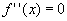 sono
le ascisse dei punti in cui la curva cambia la sua concavità, i punti di flesso,
e la tangente si dispone orizzontalmente. sono
le ascisse dei punti in cui la curva cambia la sua concavità, i punti di flesso,
e la tangente si dispone orizzontalmente.
|
|
Calcolo delle ordinate degli eventuali punti di flesso
|
Sostituisci una alla volta le ascisse dei punti di flesso nellequazione
della curva e ricava l'ordinata corrispondente.
Riporta con un segno i risultati sul grafico.
|
|
Ricerca degli eventuali asintoti obliqui
|
Se 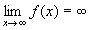 ,
allora si calcolano i due limiti : ,
allora si calcolano i due limiti :
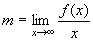 che
fornisce il coefficiente angolare m della retta, e che
fornisce il coefficiente angolare m della retta, e
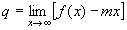 che
fornisce il valore del termine noto q della retta. che
fornisce il valore del termine noto q della retta.
Se questi due limiti esistono e sono finiti, allora la retta 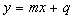 è un asintoto della curva.
è un asintoto della curva.
|
|
A questo punto dovresti avere elementi sufficienti per comporre
qualitativamente landamento della curva.
|